Answer:
The values are missing in the question. They are : 16.3,12.8,13,32.2,28.1,34.4,46.4,53,15.4,18.2
Explanation:
16.3,12.8,13,32.2,28.1,34.4,46.4,53,15.4,18.2
We calculate sample mean and std deviation from given data.
Sample Mean,
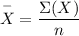 =269.8/10=26.98
=269.8/10=26.98
Sample Variance,
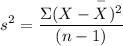 =1859.496/9=206.610667
=1859.496/9=206.610667
Sample std dev,s=
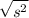 =√206.610667≈14.373958
=√206.610667≈14.373958
We want to test two tailed hypothesis:
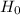 : σ=12
: σ=12
 : σ≠12
: σ≠12
Given: s=14.373958⇒
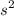 =206.610667,n=10
=206.610667,n=10
Significance level, a=0.1 Degrees of freedom, df=n-1=9
Since this is two tailed test, we need area of α=0.1 on either side of critical value. This means area of 0.05 on right of positive critical value.
Critical values are given by
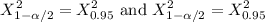 with 9 degrees of freedom.
with 9 degrees of freedom.
We can use chi-square table or following excel commands:
CHISQ. INV(0.95,9)=3.32511284307
CHISQ. INV (0.05,9)=16.9189776046
Critical Values,
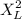 =3.325 and
=3.325 and
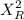 =16.919
=16.919
Since this is two tailed test, the decision rule or rejection criteria is:
Reject null hypothesis if test statistic is less than or equal to left critical value OR more than or equal to right critical value, i.e,
Reject
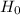 if
if
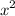 ≤3.325 OR
≤3.325 OR
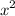 ≥16.919
≥16.919
Test statistic is given by
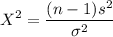 =((9)*206.610667)/144=12.913167
=((9)*206.610667)/144=12.913167
Test statistic,
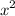 =12.913
=12.913
since test statistic is between two critical values, we (do not reject
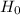 ) (i.e, we fail to reject
) (i.e, we fail to reject
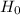 .
.
Conclusion: There is (not sufficient) evidence to conclude that standard deviation is not equal to 12 .
Alternatively, we can use p-value approach. The decision rule or rejection criteria is: reject null hypothesis if p-value is less than or equal to significance level (α), i.e, reject
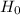 if p-value ≤0.1
if p-value ≤0.1
P-value is twice the (smaller) tail area of test statistic because this is two tailed test. We can use excel function to find this. 2*M IN (CHISQ.DIST (12.913167,9, TRUE ) 1-CHISQ.DIST 12.913167,9, TRUE ) =0.333149809868
P-value =0.3331
since p-value is greater than significance level (α),we (do not reject
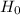 ) (i.e, we fail to reject
) (i.e, we fail to reject
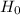 ).
).
Conclusion: There is (not sufficient) evidence to conclude that standard deviation is different from 12 .