Answer:
a) The standard form of
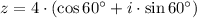 is
is
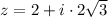 , b)
, b)
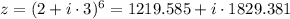 .
.
Explanation:
a) The standard form of the complex number is
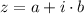 ,
,
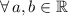 . If we get that
. If we get that
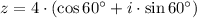 , whose standard form is obtained by algebraic means:
, whose standard form is obtained by algebraic means:
1)
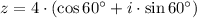 Given
Given
2)
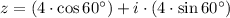 Distributive and Associative properties.
Distributive and Associative properties.
3)
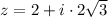 Multiplication/Result.
Multiplication/Result.
The standard form of
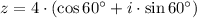 is
is
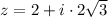 .
.
b) The De Moivre's Theorem states that:
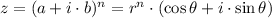
Where:
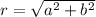 and
and
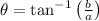 .
.
If we know that
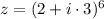 , then:
, then:
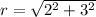
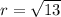
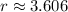
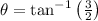
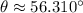
The resulting expression is:
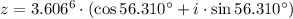
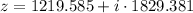
Therefore,
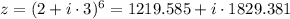 .
.