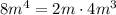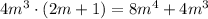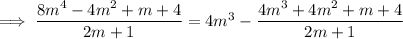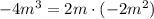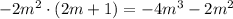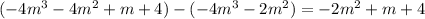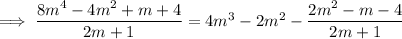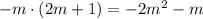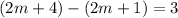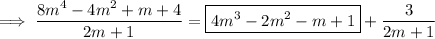Question

Find the quotient using polynomial long division:

1. (50y^3+10y^2-35y-7)divided by(5y-4)

2. (8m^4-4m^2+m+4)divided by(2m+1)

Answer 1

(1)
`50y^3=5y\cdot 10y^2`, and

`10y^2\cdot(5y-4)=50y^3-40y^2`

Subtract this from
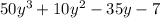`50y^3+10y^2-35y-7` to get a remainder of

`(50y^3+10y^2-35y-7)-(50y^3-40y^2)=50y^2-35y-7`

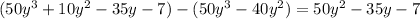
What we've done here is show that

`(50y^3+10y^2-35y-7)/(5y-4)=10y^2+(50y^2-35y-7)/(5y-4)`

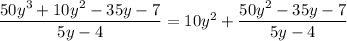
We can keep going as long as the degree of the remainder's numerator is at least the same as the degree of its denominator.

Next,
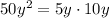`50y^2=5y\cdot 10y`, and

`10y\cdot(5y-4)=50y^2-40y`

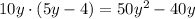
Subtract this from the previous remainder to get a new remainder of

`(50y^2-35y-7)-(50y^2-40y)=5y-7`

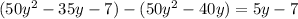
which means

`(50y^3+10y^2-35y-7)/(5y-4)=10y^2+10y+(5y-7)/(5y-4)`

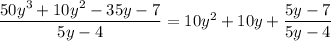
Finally,
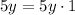`5y=5y\cdot1`, and

`1\cdot(5y-4)=5y-4`

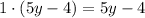
Subtract this from the previous remainder to get

`(5y-7)-(5y-4)=-3`

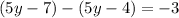
So we end up with

`(50y^3+10y^2-35y-7)/(5y-4)=\boxed{10y^2+10y+1}-\frac3{5y-4}`

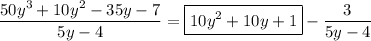
(the quotient is the expression in the box)

(2) Using the same process as before:

`8m^4=2m\cdot4m^3`

`4m^3\cdot(2m+1)=8m^4+4m^3`

`(8m^4-4m^2+m+4)-(8m^4+4m^3)=-4m^3-4m^2+m+4`

`\implies(8m^4-4m^2+m+4)/(2m+1)=4m^3-(4m^3+4m^2+m+4)/(2m+1)`

`-4m^3=2m\cdot(-2m^2)`

`-2m^2\cdot(2m+1)=-4m^3-2m^2`

`(-4m^3-4m^2+m+4)-(-4m^3-2m^2)=-2m^2+m+4`

`\implies(8m^4-4m^2+m+4)/(2m+1)=4m^3-2m^2-(2m^2-m-4)/(2m+1)`

`-2m^2=2m\cdot(-m)`

`-m\cdot(2m+1)=-2m^2-m`

`(-2m^2+m+4)-(-2m^2-m)=2m+4`

`\implies(8m^4-4m^2+m+4)/(2m+1)=4m^3-2m^2-m+(2m+4)/(2m+1)`

`2m=2m\cdot1`

`1\cdot(2m+1)=2m+1`

`(2m+4)-(2m+1)=3`

`\implies(8m^4-4m^2+m+4)/(2m+1)=\boxed{4m^3-2m^2-m+1}+\frac3{2m+1}`