Answer:
Z = -1.333
P-value = 0.09176
Decision Rule: Reject
 if ∝ is greater than the P-value
if ∝ is greater than the P-value
Conclusion: Since P-value is > the level of significance ∝, we fail to reject the null hypothesis, therefore there is insufficient evidence to conclude that at least half of all voters prefer the Democrat.
Explanation:
Given that:
The sample size of the poll = 1068
The proportion of voters that preferred Democratic candidate is
 = 0.48
= 0.48
To test the claim that at least half of all voters prefer the Democrat, i.e 1/2 = 0.5
The null hypothesis and the alternative hypothesis can be computed as:
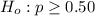
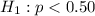
Using the Z test statistics which can be expressed by the formula:

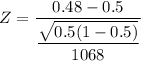
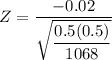
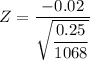
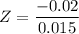
Z = -1.333
P-value = P(Z< -1.33)
From z tables,
P-value = 0.09176
The level of significance ∝ = 0.05
Decision Rule: Reject
 if ∝ is greater than the P-value
if ∝ is greater than the P-value
Conclusion: Since P-value is > the level of significance ∝, we fail to reject the null hypothesis, therefore there is insufficient evidence to conclude that at least half of all voters prefer the Democrat.