Given :
A particle moves in the xy plane starting from time = 0 second and position (1m, 2m) with a velocity of v=2i-4tj .
To Find :
A. The vector position of the particle at any time t .
B. The acceleration of the particle at any time t .
Solution :
A )
Position of vector v is given by :
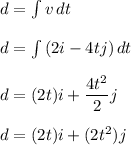
B )
Acceleration a is given by :
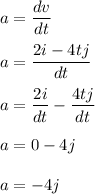
Hence , this is the required solution .