Question

Solve the given inequality.
4.2x > 6.3

Answer 1

`\huge\boxed{x>1(1)/(2)\to x\in\left(1(1)/(2),\ \infty\right)}`

Explanation:

`4.2x>6.3\qquad/\text{divide both sides by 4.2}\\\\(4.2x)/(4.2)>(6.3)/(4.2)\\\\x>(6.3\cdot10)/(4.2\cdot10)\\\\x>(63:21)/(42:21)\\\\x>(3)/(2)\\\\x>1(1)/(2)`

Answer 2

x > 1.5

Explanation:

In order to solve for x, we must isolate x on one side of the inequality.

`4.2x > 6.3`

x is being multiplied by 4.2 The inverse of multiplication is division. Divide both sides of the equation by 4.2

`(4.2x)/(4.2) >(6.3)/(4.2)`

`x> (6.3)/(4.2)`

`x> 1.5`

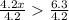
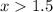
The solution to the inequality 4.2x > 6.3 is x>1.5