Question

Consider the following statements. Select all that are always true.

- The sum of a rational number and a rational number is rational.
- The sum of a rational number and an irrational number is irrational.
- The sum of an irrational number and an irrational number is irrational. - The product of a rational number and a rational number is rational.
- The product of a rational number and an irrational number is irrational. - The product of an irrational number and an irrational number is irrational.

Answer 1

hey! just wanted to let you know that an irrational number times a rational number can be rational.

Explanation:

Rational is anything you can write as a fraction. Irrational is something you cannot write as a fraction. That being said, you can write 0 as a fraction (0/1=0), this means that when you multiply any irrational number times 0, the answer will always come back to 0, meaning an irrational times a rational is open under multiplication.

Answer 2

A, B, D and E

Explanation:

Given

Options A to F

Required

Determine which is true

Option A:

This is always true;

Take for instance the following rational numbers

`a = (1)/(2)`
`b = (1)/(3)`

`a + b = (1)/(2) + (1)/(3)`

`a + b = (3 + 2)/(6)`

`a + b = (5)/(6)`

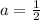
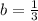
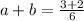
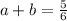
This will always result in a rational number

Option B:

This is always true;

Take for instance the following rational number

`a = 0.5`

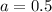
And the following irrational number

`b = 3.142857`

`a + b =0.5+ 3.142857`

`a + b =3.642857`

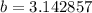
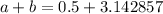
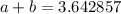
This will always result in an irrational number

Option C:

This is not always true;

1. Take for instance the following irrational numbers

`a = 0.33333`
`b = 3.142857`

`a + b =0.33333 + 3.142857`

`a + b =3.476187`

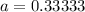
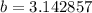
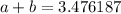
2. Take for instance the following irrational numbers

`a = 3 + \sqrt5`
`b = -\sqrt5`

`a + b = 3 + \sqrt5 - \sqrt5`

`a + b = 3`

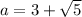
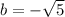
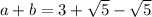
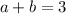
From the above examples, this implies that the statement is not always true

D.

This is always true;

Take for instance the following rational numbers

`a = (1)/(2)`
`b = (1)/(3)`

`a * b = (1)/(2) * (1)/(3)`

`a * b = (1)/(6)`

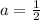
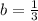
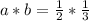
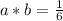
This will always result in a rational number

E.

This is always true;

Take for instance the following rational number

`a = 0.5`

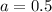
And the following irrational number

`b = 3.142857`

`a * b =0.5 * 3.142857`

`a * b =1.5714285`

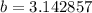
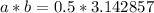
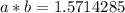
This will always result in an irrational number

F.

This is not always true;

1. Take for instance the following irrational numbers

`a = 0.33333`
`b = 3.142857`

`a * b =0.33333 * 3.142857`

`a * b =1.04760852381`

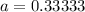
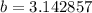
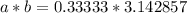
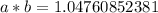
2. Take for instance the following irrational numbers

`a = 3 + \sqrt5`
`b = 0`

`a * b = (3 + \sqrt5) * 0`

`a * b = 0`

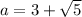
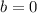
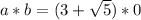
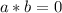
From the above examples, this implies that the statement is not always true