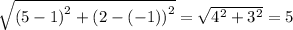Question

Find k so that the distance from (–1, 1) to (2, k) is 5 units.

Answer 1

k = -3 or 5

Explanation:

The given parameters are;

The line extends from points (-1, 1) to point (2, k)

The length of the line = 5 units

The formula for the length, l, of a line given its coordinates can be found by the following formula;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

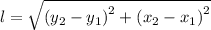
Therefore, we have;

`5 = \sqrt{\left (k-1 \right )^(2)+\left (2-(-1) \right )^(2)}`

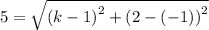
Which, by squaring both sides, gives;

25 = (k - 1)² + (2 - (-1))² = (k - 1)² + (2 + 1)² = (k - 1)² + 3²

25 = (k - 1)² + 3² = k² - 2·k + 1 + 9

25 - 25 = 0 = k² - 2·k + 1 + 9 - 25 = k² - 2·k - 15

0 = k² - 2·k - 15

0 = (k +3) × (k - 5)

Therefore, k = -3 or 5

When k - -3, we have;

`\sqrt{\left ((-3)-1 \right )^(2)+\left (2-(-1) \right )^(2)}= √((-4)^2+3^2) = √(16 + 9) = √(25) = 5`

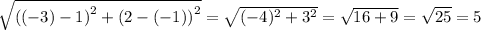
When k = 5, we have;

`\sqrt{\left (5-1 \right )^(2)+\left (2-(-1) \right )^(2)}= √(4^2+3^2) = 5`