Answer:

Explanation:
The sum of an infinite geometric series is expressed according to the formula;
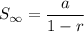 where;
where;
a is the first term of the series
r is the common ratio
If the sum of an infinite geometric series is three times the first term, this is expressed as
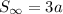
Substitute
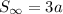 into the formula above to get the common ratio r;
into the formula above to get the common ratio r;
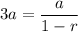
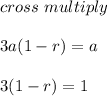
open the parenthesis
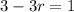
subtract 3 from both sides
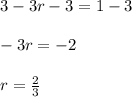
Hence the common ratio of this series is
