Given :
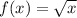
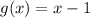
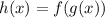
To Find :
Find h(x).
What is the domain of h(x).
Find h(2) and h(0).
Solution :
a )
Now , h(x) is given by :
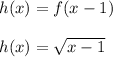
b )
We know , square root of negative number is not defined .
So, x-1 ≥ 0
x ≥ 1
Therefore , the domain of h(x) is [ 1 , ∞ ) .
c )
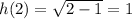
Since , domain of h(x) is [ 1 , ∞ ) .
Therefore , function has no value for 0 .
Hence , this is the required solution .