Question

Express 3/x²-9 into partial fraction​

Answer 1

Hope this can help.

Answer 2

Hi there!

~

⇒
`- (1)/(2(x + 3)) + (1)/(2(x - 3))`

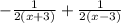
Step by Step :

∴ Factor
`x^2 - 9` :
`( x+ 3 ) ( x - 3)`

`= (3)/((x +3)(x - 3))`

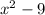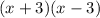
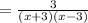
∴ Create the partial fraction template using the denominator
`( x + ) ( x - 3)`

`(3)/(( x + 3) ( x -3)) = (a^0)/(x + 3) + (a^1)/(x - 3)`

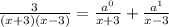
∴ Multiply the equation by the denominator.

`(3(x+3)(x-3))/(( x+3)(x-3)) = (a^0(x +3)(x-3))/(x + 3) + (a^1 (x+3)(x-3))/(x - 3)`

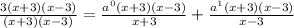
∴ Simplify.

`3 = a^0 ( x - 3) + a^1 ( x+3)`

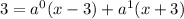
∴ Solve the unknown parameters by plugging the real roots of the denominator : - 3,3

⇅

∴ Solve the denominator root -3 :
`a^0 = -(1)/(2)`

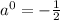
∴ For the denominator root 3 :
`a^1 = (1)/(2)`

`a^0 = -(1)/(2) , a^1 (1)/(2)`

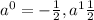
∴Plug the solutions to the partial fraction parameters to obtain the final result.

`((-(1)/(2)) )/(x + 3) + ((1)/(2) )/( x- 3)`

∴ Simplify

`- (1)/(2(x + 3)) + (1)/(2(x - 3))`

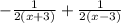
Hope this helped you!