The factored form of the trinomial is (5x - 2)(x - 6).
The image you sent shows a question from a math homework assignment:
Factor the trinomial by grouping:
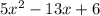
To factor a trinomial by grouping, we first need to find two numbers whose product is the coefficient of our x^2 term (5) and whose sum is the coefficient of our x term (-13). In this case, those two numbers are -2 and -6.
Next, we write the trinomial as two pairs of terms, with the two numbers we just found in the middle:
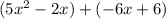
We can then factor out the common factors in each pair of terms:
x(5x - 2) - 6(5x - 2)
Finally, we can notice that the common factor (5x - 2) appears in both terms. Factoring this out, we get:
(5x - 2)(x - 6)
Therefore, the factored form of the trinomial is (5x - 2)(x - 6).
Here is a more detailed explanation of each step:
Find two numbers whose product is the coefficient of the
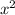term and whose sum is the coefficient of the x term.
This can be done by trial and error, or by using a factoring method such as the sum-product pattern.
Write the trinomial as two pairs of terms, with the two numbers you just found in the middle.
This is simply a matter of rearranging the terms of the trinomial.
Factor out the common factors in each pair of terms.
This is done using the distributive property.
Look for common factors between the factored forms of the paired terms.
If there are any common factors, factor them out.
This is a general method for factoring trinomials by grouping. It can be applied to any trinomial, regardless of the coefficients.