Question

Someone please help me

Answer 1

8. Louis

9. Rose; Raymond

Explanation:

8. An exponent represents the number of times the base appears as a factor in the product.

We use a coefficient to signify repeated addition: 3x means x+x+x.

We use an exponent to signify repeated multiplication. x³ means x·x·x.

So, the expression ...

`4^2\cdot 4^5\text{ means }(4\cdot4)\cdot(4\cdot4\cdot4\cdot4\cdot4)`

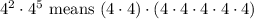
You can see that the factor 4 appears 7 times in the product, so would be represented in exponential form as ...

`4^2\cdot4^5=\boxed{4^7}`

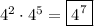
Louis has correctly observed this fact. In general, we see that multiplying powers of the same base causes those powers to be added.

__

9.

Part A. Rose is correct for the same reason as in problem 8.

5^5 · 5^2 = 5^(5+2) = 5^7

Part B. Raymond is correct. We know that division cancels similar terms from the numerator, so ...

`(7^9)/(7^5)=(7\cdot7\cdot7\cdot7\cdot7\cdot7\cdot7\cdot7\cdot7)/(7\cdot7\cdot7\cdot7\cdot7)=7\cdot7\cdot7\cdot7=7^(9-5)=7^4`

__

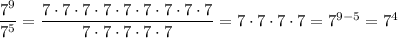
The rules of exponents we're using here are ...

(a^b)(a^c) = a^(b+c)

(a^b)/(a^c) = a^(b-c)