Question

The following equation of a quadratic function is given in standard form. f(x) = x²- 2x + 2 Determine the vertex for each quadratic. Round your answers to the nearest tenth if necessary. (x, y) = ______.

Answer 1

The vertex for each quadratic is
`(x,y) = (1,1)`

Explanation:

To determine the vertex for each quadratic,

The vertex of the
`x` coordinate can be determined using the formula,

`x-vertex = (-b)/(2a)`

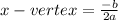
The standard form of the quadratic function is

`f(x) = ax^(2) + bx + c`

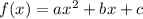
Hence, for the given equation of the quadratic function,

`f(x) = x^(2) -2x +2`

`a = 1`

`b = -2`

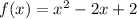
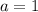
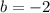
and
`c = 2`

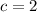
Hence,
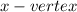`x-vertex` becomes,

`x-vertex = (-b)/(2a)`

`x-vertex = (--2)/(2(1))`

`x-vertex = (2)/(2)`

∴
`x - vertex = 1`

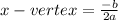
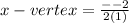
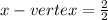
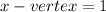
This is the vertex for the
`x-coordinate`

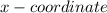
To determine, the vertex for the
`y-coordinate`

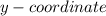
We will put the value of the vertex of the
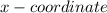`x-coordinate` in the equation and write

`y-vertex = x^(2) - 2x + 2`

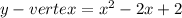
Then,

`y-vertex = (1)^(2) -2(1) + 2`

`y-vertex = 1 - 2 +2\\y-vertex = 1`

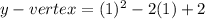
This the vertex for the
`y-coordinate`

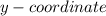
Hence,
`(x,y) = (1,1)`