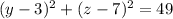Question

Find an equation of the sphere with center (−2, 3, 7) and radius 7.What is the intersection of this sphere with the yz-plane?

Answer 1

The equation of the sphere with center (-2, 3, 7) and radius 7 is
`(x+2)^(2)+(y-3)^(2)+(z-7)^(2) = 49`.

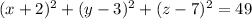The intersection of the sphere with the yz-plane is
`(y-3)^(2)+(z-7)^(2) = 49`.

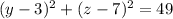Explanation:

We know that any sphere can be represented by the following equation:

`(x-h)^(2)+(y-k)^(2)+(z-s)^(2) = r^(2)`

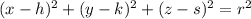
Where:

`h`,
`k`,
`s` - Coordinates of the center of the sphere, dimensionless.

`r` - Radius of the sphere, dimensionless.

If
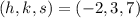`(h,k, s) = (-2,3,7)` and
`r = 7`, we obtain this expression:

`(x+2)^(2)+(y-3)^(2)+(z-7)^(2) = 49`

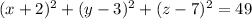
The intersection of the sphere with the yz-plane observe the following conditions:

`x = 0`,
`y \in \mathbb {R}`,
`z\in \mathbb{R}`

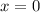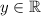Hence, the expression above can be reduced into this:

`(y-3)^(2)+(z-7)^(2) = 49`