Question

(look at the images) can i get help on these?

Answer 1

see explanation

Explanation:

15

JK + KL = JL , substitute values

2x + 1 + 6x = 81, that is

8x + 1 = 81 ( subtract 1 from both sides )

8x = 80 ( divide both sides by 8 )

x = 10

Thus JK = 2x + 2 = 2(10) + 1 = 20 + 1 = 21

KL = 6x = 6 × 10 = 60

--------------------------------------------------------------

16

JK + KL = JL , substitute values

2x + x + 2 = 5x - 10 , that is

3x + 2 = 5x - 10 ( subtract 3x from both sides )

2 = 2x - 10 ( add 10 to both sides )

12 = 2x ( divide both sides by 2 )

6 = x

Thus

JK = 2X = 2 × 6 = 12

KL = x + 2 = 6 + 2 = 8

JL = 5x - 10 = 5(6) - 10 = 30 - 10 = 20

------------------------------------------------------------

17

Calculate the distance d using the distance formula

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

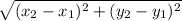
with (x₁, y₁ ) = S(7, 3) and (x₂, y₂ ) = T(1, - 5)

d =
`√((1-7)^2+(-5-3)^2)`

=
`√((-6)^2+(-8)^2)`

=
`√(36+64)`

=
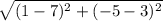
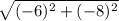
`√(100)` = 10