Question

Write the equation of a line

Answer 1

Answer: Option D.

Explanation:

Hey there!!

Here, To find the equation of a st.line passing through point (3,1) is :

`(y - 1) = m1(x - 3)`

It is the first equation.

Given, Another equation is:

`y = (2)/(3) x + 1`

It is 2nd equation.

Comparing the 2nd equation with y = mx+c we get,

Slope (m2) = 2/3.

As per the condition of parallel lines,

m1 = m2 = 2/3.

Putting, the value of m1 in equation 1st we get,

`(y - 1) = (2)/(3) (x - 3)`

or, 3 (y-1) = 2(x-3)

or, 3y - 3 = 2x - 6

`y = (2x - 6 + 3)/(3)`

`y = (2)/(3) x - 1`

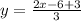
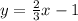
Diving-3/3 = -1.

Therefore, y = 2/3 x - 1 is the required equation.

Hope it helps.