Question

The manager of a restaurant found that the cost to produce 200 cups of coffee is ​$65.00 ​, while the cost to produce 250 cups is ​$77.50 . Assume the relationship between the cost y to produce x cups of coffee is linear. a. Write a linear equation that expresses the​ cost, y, in terms of the number of cups of​ coffee, x. b. How many cups of coffee are produced if the cost of production is ​$135.00 ​?

Answer 1

a). y = 0.25x + 15

b). x = 480 cups

Explanation:

(a). Let the equation of the linear function passing through a point (x', y') is,

y - y' = m(x - x')

'm' = slope of the line

b = y-intercept

Two points lying on the linear function will be (200, 65) and (250, 77.5).

Slope of the line 'm' =
`(y_2-y_1)/(x_2-x_1)`

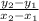
m =
`(77.5-65)/(250-200)`

=
`(12.5)/(50)`

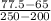
= 0.25

Therefore, equation of the line passing through (200, 65) and slope 0.25 will be,

y - 65 = 0.25(x - 200)

y - 65 = 0.25x - 50

y = 0.25x + 15

(b). For y = $135 we have to calculate the number of cups of coffee produced.

135 = 0.25x + 15

0.25x = 135 - 15

0.25x = 120

x = 480 cups

Therefore, 480 cups of coffee will be produced.