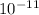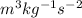Answer:
G = 1.670 ×
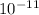
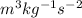
Step-by-step explanation:
From Newton's law of universal gravitation,
F =

Where F is the force of attraction, G is the gravitational constant, M is the mass of the earth, R is the radius of the earth.
From Newton's second law of motion,
F = mg
mg =

g =

⇒ G =
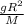
If the radius of the earth becomes half,
R =
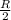 , then;
, then;
G =
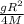
Given that: g = 9.8 m/
 , radius of the earth is 6371000 m, mass of the earth is 5.972 ×
, radius of the earth is 6371000 m, mass of the earth is 5.972 ×
 kg, then;
kg, then;
G =
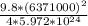
= 1.670 ×