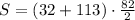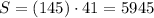Answer:
5945
Explanation:
The sum for an arithmetic series is given by the formula:
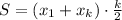
Where x₁ is the initial term, x_k is the last term, and k is the number of elements in the series.
From the sequence, we can see that the first term is 32. The last term is 113.
To determine how many elements we have, subtract 113 and 32:
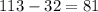
However, we must add 1 to this number since this doesn't include the first term. Thus:
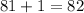
So, there are 82 terms in total.
Therefore, our sum is: