Question

Two hikers are 22 miles apart and walking toward each other. They meet in 5 hours. Find the rate of each hiker if one hiker walks 2.2 mph faster than the other

Answer 1

The hikers A and B travel at rates of 1.1 miles per hour and 3.3 miles per hour, respectively.

Explanation:

Let suppose that each hiker travels at constant speed, such that kinematic formulas are, respectively:

Hiker A

`x_(A) = x_(A,o)+v_(A)\cdot t`

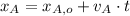
Hiker B

`x_(B) = x_(B,o) +v_(B)\cdot t`

Relationship

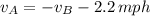`v_(A) =- v_(B)-2.2\,mph` (They walk toward each other)

Where:

`x_(A,o)`,
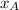`x_(A)` - Initial and final position of the hiker A, measured in miles.

`x_(B,o)`,
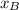`x_(B)` - Initial and final position of the hiker B, measured in miles.

`t` - Time, measured in hours.

`v_(A)`,
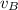`v_(B)` - Velocities of hikers A and B, measured in miles per hour.

Given that
`x_(A,o) = 0\,mi`,
`x_(B,o) = 22\,mi`,
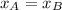`x_(A) = x_(B)` and
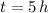`t = 5\,h`, the system of equation is reduced to the following:

`0\,mi -(v_(B)+2.2\,mph)\cdot (5\,h) = 22\,mi+v_(B)\cdot (5\,h)`

`-5\cdot v_(B)-11 = 22+5\cdot v_(B)`

`10\cdot v_(B) = -33`

`v_(B) = -3.3\,mph`

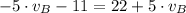
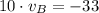
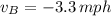
Now, the velocity of the hiker A is:

`v_(A) = - (-3.3\,mph)-2.2\,mph`

`v_(A) = 1.1\,mph`

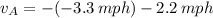
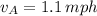
The hikers A and B travel at rates of 1.1 miles per hour and 3.3 miles per hour, respectively.