Answer:
Null hypothesis:
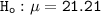
Alternative hypothesis
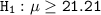
t = -0.080
Decision Rule: To reject the null hypothesis if t > 1.340 at t
Since t = -0.080, this implies that t < 1.340 that means the t statistics value did not fall into the rejection region. Hence, we fail to reject the null hypothesis at the level of significance 0.10
Conclusion: We conclude that there is insufficient evidence to support the claim that the mean nickel diameter drawn by children in the low-income group is greater than 21.21 mm.
Explanation:
Given that:
the sample mean
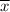 = 21.15
= 21.15
the standard deviation
 = 4.7512
= 4.7512
sample size N = 40
The objective is to test the claim that the mean nickel diameter drawn by children in the low-income group is greater than 21.21 mm.
At the level of significance of 0.1
The null hypothesis and the alternative hypothesis for this study can be computed as follows:
Null hypothesis:
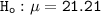
Alternative hypothesis
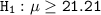
This test signifies a one-tailed test since the alternative is greater than or equal to 21.21
The t-test statistics can be computed by using the formula:
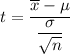
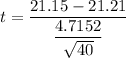

t = -0.080
degree of freedom = n - 1
degree of freedom = 40 - 1
degree of freedom = 39
From the t statistical tables,
at the level of significance ∝ = 0.1 and degree of freedom df = 39, the critical value of

Decision Rule: To reject the null hypothesis if t > 1.340 at t
Since t = -0.080, this implies that t < 1.340 that means the t statistics value did not fall into the rejection region. Hence, we fail to reject the null hypothesis at the level of significance 0.10
Conclusion: We conclude that there is insufficient evidence to support the claim that the mean nickel diameter drawn by children in the low-income group is greater than 21.21 mm.