Question

Find the length of the segment. Round your answer to the nearest tenth. ​

Answer 1

The length of the line segment: 5.8 units

Explanation:

To find the length of a line segment, you must us the formula:

D=
`√((x_2-x_1)^2+(y_2-y_1)^2)`

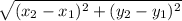
1. well, you must first identify your coordinates

Point A is (-2, -4) which is (
`x_1`,
`y_1`)

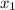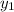Point B is (1, 1) which is (
`x_2`,
`y_2`)

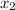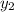2. Now you put these coordinates into your equation

D=
`√((1--2)^2+(1--4)^2)`

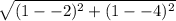
Ofc, you gotta keep in mind of any double negatives

D=
`√((1+2)^2+(1+4)^2)`

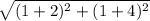
3. simplify

D=
`√((3)^2+(5)^2)`

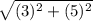
D=
`√(9+25)`

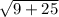
D=
`√(34)`

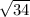
The square root of 34 is 5.83095189.... in decimal form

4. Round it to the nearest tenth

5.83 and since 3 is lower than five, it does nothing

5.8= The length of your line segment!