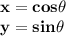Question

Solve the system of linear equations for x and y.(cos θ)x + (sin θ)y=1(−sin θ)x + (cos θ)y = 0x=y=

Answer 1

`\bold{x =cos\theta}\\\bold{y=sin\theta}`

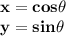
Explanation:

The given system of linear equations is:

`(cos\theta)x+(sin\theta)y=1\\(-sin\theta)x+(cos\theta)y=0`

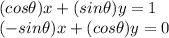
We have to solve the equations for the values of
`x, y`.

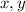Let us use elimination method in which we eliminate one of the variables from the two variables.

For this, let us multiply the first equation by
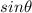`sin\theta` and second equation by
`cos\theta`

Now, the equations become:

`(cos\theta.sin\theta)x+(sin\theta.sin\theta)y=sin\theta\\\Rightarrow (cos\theta.sin\theta)x+(sin^2\theta)y=sin\theta ....... (1)\\\\(-sin\theta.cos\theta)x+(cos\theta.cos\theta)y=0\\\Rightarrow (-sin\theta.cos\theta)x+(cos^2\theta)y=0 ..... (2)`

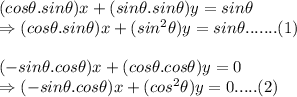
Now, let us add (1) and (2):

`(sin^2\theta)y+(cos^2\theta)y=sin\theta\\\Rightarrow (sin^2\theta+cos^2\theta)y=sin\theta\\\Rightarrow (1)y=sin\theta\\\Rightarrow y = sin\theta`

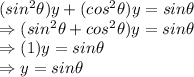
Using the equation:

`(-sin\theta)x+(cos\theta)y=0`

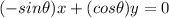
Putting value of
`y`:

`\Rightarrow (-sin\theta)x+(cos\theta)sin\theta=0\\\Rightarrow (sin\theta)x=(cos\theta)sin\theta\\\Rightarrow x = cos\theta`

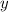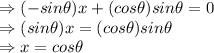
So, the answer to the system of linear equations is:

`\bold{x =cos\theta}\\\bold{y=sin\theta}`