Question

Let ABC be a triangle such that AB=13 BC=14 and CA=15. D is a point on BC such that AD Bisects

Answer 1

Area of triangle ADC is 54 square unit

Explanation:

Here is the complete question:

Let ABC be a triangle such that AB=13, BC=14, and CA=15. D is a point on BC such that AD bisects angle A. Find the area of triangle ADC .

Explanation:

Please see the attachment below for an illustrative diagram

Considering the diagram,

BC = BD + DC = 14

Let BD be
`x` ; hence, DC will be
`14-x`

and AD be
`y`

To, find the area of triangle ADC

Area of triangle ADC =
`(1)/(2) (DC)(AD)`

=
`(1)/(2)(14-x)(y)`

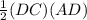
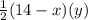
We will have to determine
`x` and
`y`

First we will find the area of triangle ABC

The area of triangle ABC can be determined using the Heron's formula.

Given a triangle with a,b, and c

`Area =√(s(s-a)(s-b)(s-c))`

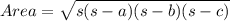
Where
`s = (a+b+c)/(2)`

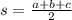
For the given triangle ABC

Let
`a` = AB,
`b` = BC, and
`c` = CA

Hence,
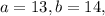`a = 13, b= 14,` and
`c = 15`

∴
`s = (13+14+15)/(2) \\s= (42)/(2)\\s = 21`

Then,

Area of triangle ABC =
`√((21)(21-13)(21-14)(21-15))`

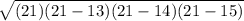
Area of triangle ABC =
`√((21)(8)(7)(6))` =
`√(7056)`

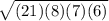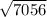
Area of triangle ABC = 84 square unit

Now, considering the diagram

Area of triangle ABC = Area of triangle ADB + Area of triangle ADC

Area of triangle ADB =
`(1)/(2) (BD)(AD)`

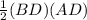
Area of triangle ADB =
`(1)/(2)(x)(y)`

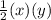
Hence,

Area of triangle ABC =
`(1)/(2)(x)(y)` +
`(1)/(2)(14-x)(y)`

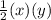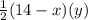
84 =
`(1)/(2)(x)(y)` +
`(1)/(2)(14-x)(y)`

∴
`84 = (1)/(2)(xy) + 7y - (1)/(2)(xy)`

`84 = 7y\\y = (84)/(7)`

∴
`y = 12`

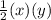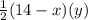
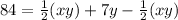
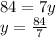
Hence,
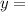`y =` AD = 12

Now, we can find BD

Considering triangle ADB,

From Pythagorean theorem,

/AB/² = /AD/² + /BD/²

∴13² = 12² + /BD/²

/BD/² = 169 - 144

/BD/ =
`√(25)`

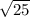
/BD/ = 5

But, BD + DC = 14

Then, DC = 14 - BD = 14 - 5

BD = 9

Now, we can find the area of triangle ADC

Area of triangle ADC =
`(1)/(2) (DC)(AD)`

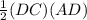
Area of triangle ADC =
`(1)/(2) (9)(12)`

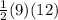
Area of triangle ADC = 9 × 6

Area of triangle ADC = 54 square unit

Hence, Area of triangle ADC is 54 square unit.