Question

The meter was originally defined so that the period of a meter-long simple pendulum would be exactly 2.00 second. (Was your measured value close to this?) Given the relationship, T^2 alpha L (T^2 is proportional to L) what would be the length of a simple pendulum, in centimeters, with a period of exactly one second?

Answer 1

Step-by-step explanation:

Given that,

Initial length of simple pendulum,
`L_1=1\ m`

Initial time period,
`T_1=2\ s`

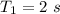
We need to find the length of the simple pendulum when the period is exactly 1 second.

`T_2=1\ s`

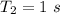
We know that the time period of simple pendulum is given by :

`T=2\pi \sqrt{(L)/(g)} \\\\T\propto √(L) \\\\(T_1)/(T_2)=(L_1)/(L_2)`

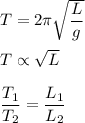
Put all values and find L₂

`(T_1)/(T_2)=\sqrt{(L_1)/(L_2)}\\\\L_2=(T_2^2L_1)/(T_1^2)\\\\L_2=(1^2* 100\ cm)/(2^2\ s)\\\\L_2=25\ cm`

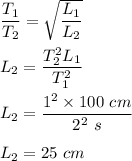
So, the length of the pendulum with a period of exactly one second is 25 cm.