Question

Simplify :
Stepwise answer! ​

Answer 1

`\boxed{ \bold{ \huge{ \boxed{ \sf{ \frac{14 {x}^(2) - 96}{ {x}^(4) - 13 {x}^(2) + 36}}}}}}`

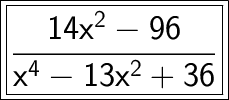
Explanation:

`\sf{ (2)/(x - 2) + (1)/(x - 3) - (2)/( x + 2) - (1)/( x + 3)}`

⇒
`\sf{ (2(x - 3)(x + 3)(x + 2) + (x - 2)(x + 2)(x + 3) - 2(x - 2)(x - 3)(x + 3) - (x - 2)(x + 2)(x - 3))/((x - 2)(x - 3)(x + 2)(x + 3))}`

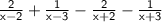
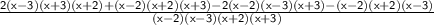
Use the formula : a² - b² = ( a + b ) ( a - b )

⇒
`\sf{ \frac{2( {x}^(2) - 9)(x + 2) + ( {x}^(2) - 4)(x + 3) - (2x - 4)( {x}^(2) - 9) - ( {x}^(2) - 4)(x - 3) }{( {x}^(2) - 4)( {x}^(2) - 9)}}`

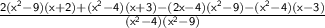
Distribute 2 through the parentheses

⇒
`\sf{ \frac{(2 {x}^(2) - 18)(x + 2) + ( {x}^(2) - 4)(x + 3) - (2x - 4)( {x}^(2) - 9) - ( {x}^(2) - 4)(x - 3)}{( {x}^(2) - 4)( {x}^(2) - 9) } }`

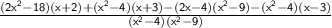
Multiply the algebraic expressions

⇒
`\sf{ \frac{2 {x}^(3) + 4 {x}^(2) - 18x - 36 + {x}^(3) + 3 {x}^(2) - 4x - 12 - (2 {x}^(3) - 18x - 4 {x}^(2) + 36) - ( {x}^(3) - 3 {x}^(2) - 4x + 12) } {( {x}^(2) - 4)( {x}^(2) - 9)} }`

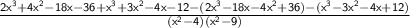
When there is a ( - ) in front of an expression, change the sign of each term in the expression

⇒
`\sf{ \frac{2 {x}^(3) + 4 {x}^(2) - 18x - 36 + {x}^(3) + 3 {x}^(2) - 4x - 12 - 2 {x}^(3) + 18x + 4 {x}^(2) - 36 - {x}^(3) + 3 {x}^(2) + 4x - 12}{( {x}^(2) - 4)( {x}^(2) - 9) } }`

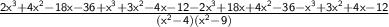
Since two opposites add up to zero, it would be better to remove them from the expression

⇒
`\sf{ \frac{4 {x}^(2) - 36 + 3 {x}^(2) - 12 + 4 {x}^(2) - 36 + 3 {x}^(2) - 12}{( {x}^(2) - 4)( {x}^(2) - 9)} }`

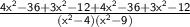
collect like terms and simplify

⇒
`\sf{ \frac{14 {x}^(2) - 48 - 36 - 12}{( {x}^(2) - 4)( {x}^(2) - 9) } }`

⇒
`\sf{ \frac{14 {x}^(2) - 84 - 12}{( {x}^(2) - 4)( {x}^(2) - 9) } }`

⇒
`\sf{ \frac{14 {x}^(2) - 96}{ ({x}^(2) - 4)( {x}^(2) - 9)} }`

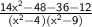
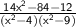
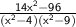
Multiply : ( x² - 4 ) and ( x² - 9 )

⇒
`\sf{ \frac{14 {x}^(2) - 96}{ {x}^(4) - 13 {x}^(2) + 36}}`

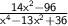
Hope I helped!

Best regards! :D