Question

17. Write a quadratic equation to find two consecutive odd natural numbers whose

product is 63. Then find the numbers

Answer 1

7 and 9

Explanation:

So we want two consecutive odd numbers whose product is 63.

Let's write an equation.

Let's let n be a random integer: doesn't matter what it is. Therefore, the first integer must be 2n+1.

This is because we're letting n be whatever it wants to be. If we multiply that whatever number by 2, then it will turn even. If we add 1 to an even number, it becomes odd.

Therefore, our first odd number is (2n+1). Our second, then, must be (2n+3).

Multiply them together. They equal 63. Thus:

`(2n+1)(2n+3)=63`

Expand:

`4n^2+6n+2n+3=63`

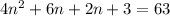
Combine like terms:

`4n^2+8n+3=63`

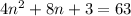
Subtract 63 from both sides:

`4n^2+8n-60=0`

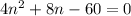
Divide both sides by 4:

`n^2+2n-15=0`

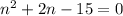
And now, factor:

`(n+5)(n-3)=0`

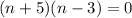
Zero Product Property:

`n+5=0\text{ or } x-3=0`

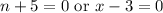
Find n:

`n=-5\text{ or } n=3`

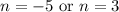
So, we've found n.

Then the first integer is either:

`2(-5)+1 \text{ or } 2(3)+1`

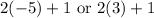
Evaluate:

`-9 \text{ or } 7`

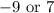
However, we want two consecutive odd natural numbers. So, ignore the -9.

Therefore, our first odd integer is 7.

And our second one would be 9.

So, our answer is 7 and 9.

And we're done!