Question

In the drawing above two rugby players start 41 meters apart at rest. Player 1 accelerates at 2.2 m/s^2 and player 2 accelerates at 1.7 m/s^2. How much time elapses before the players collide?

Answer 1

The time that elapses before the players collide is 4.59 secs

Explanation:

The distance between the two players is 41 meters. Hence, they would have total distance of 41 meters by the time they collide.

We can write that

S₁ + S₂ = 41 m

Where S₁ is the distance covered by Player 1 before collision

and S₂ is the distance covered by Player 2 before collision

From one of the equations of kinematics for linear motion,

`S = ut` +
`(1)/(2) at^(2)`

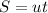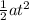
Where
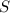`S` is distance

`u` is the initial velocity

`a` is acceleration

and
`t` is time

Since the players collide at the same time, then time spent by player 1 before collision equals time spent by player 2 before collision

That is, t₁ = t₂ = t

Where t₁ is the time spent by player 1

and t₂ is the time spent by player 2

For player 1

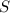`S` = S₁

`u` = 0 m/s ( The player starts at rest)

`a` = 2.2 m/s²

Then,

S₁ =
`0(t)` +
`(1)/(2) (2.2)t^(2)`

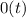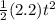
S₁ =
`1.1t^(2)`

`t^(2) = (S_(1) )/(1.1)`

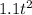
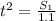
For player 2

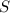`S` = S₂

`u` = 0 m/s ( The player starts at rest)

`a` = 1.7 m/s²

Then,

S₂ =
`0(t)` +
`(1)/(2) (1.7)t^(2)`

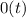S₂ =
`0.85t^(2)`

`t^(2) = (S_(2) )/(0.85)`

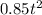
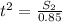
Since the time spent by both players is equal, We can write that

`t^(2)` =
`t^(2)`

Then,

`(S_(1) )/(1.1) = (S_(2) )/(0.85)`

`0.85S_(1) = 1.1S_(2)`

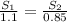
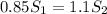
From, S₁ + S₂ = 41 m

S₂ = 41 - S₁

Then,

`0.85S_(1) = 1.1 ( 41 -S_(1) )`

`0.85S_(1) = 45.1 - 1.1S_(1)`

`0.85S_(1) + 1.1S_(1) = 45.1 \\1.95S_(1) = 45.1\\S_(1) = (45.1)/(1.95) \\S_(1) = 23.13 m`

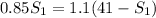
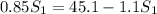
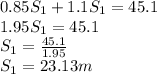
This is the distance covered by the first player. We can then put this value into
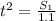`t^(2) = (S_(1) )/(1.1)` to determine how much time elapses before the players collide.

`t^(2) = (S_(1) )/(1.1)`

`t^(2) = (23.13 )/(1.1)`

`t^(2) = 21.03\\t = √(21.03) \\t = 4.59 secs`

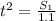
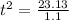
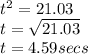
Hence, the time that elapses before the players collide is 4.59 secs