Answer: Choice B
The equation is sometimes true. When x = 0, 1 or -1, then the equation is true. Otherwise, the equation is false.
====================================================
Step-by-step explanation:
When it comes to something like "always true" all we need is one counter example to break that statement. Pick something like x = 64 and you'll find that the left hand side becomes
![x^(1/3) = 64^(1/3) = \sqrt[3]{64} = \sqrt[3]{4^3} = 4](https://img.qammunity.org/2021/formulas/mathematics/college/fluryr9vnr3geyugrzkckutnzvgpim8iy2.png)
while the right hand side turns into

This means the original equation
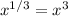 updates to
updates to
 after plugging in x = 4. We get a false statement making the original statement false when x = 4. So saying "
after plugging in x = 4. We get a false statement making the original statement false when x = 4. So saying "
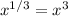 is always true" is not correct.
is always true" is not correct.
----------------------
The equation is only sometimes true for the x values 0, 1 and -1
Let's try x = 0

we get a true statement confirming x = 0 as a solution
Trying x = 1 leads to
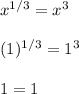
also true. A similar situation happens with x = -1 as well, just that we have negatives this time.