Question

A radio tower is 100 feet tall. A guy wire runs 135 feet, from point A at the top of the tower, to the ground at point B The base of the

radio tower is at point C. Triangle ABC is a right triangle.
How far IS from the base of the radio tower to point B where the guy wire secured to the ground? Round to the nearest tenth of a
foot

Answer 1

• P=100ft
• H=135ft

We need base

Apply Pythagorean theorem

• B²=H²-P²
• B²=135²-100²
• B²=18225-10000
• B²=8225
• B=90.697ft
• B=90.7ft

Answer 2

90.7 ft (nearest tenth)

Explanation:

From the given information, this can be modeled as a right triangle, where:

• AB = hypotenuse = 135 ft
• AC = height = 100 ft
• BC = base

To find the base of the triangle (BC), use Pythagoras' Theorem

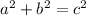`a^2+b^2=c^2` (where a and b are the legs, and c is the hypotenuse)

`\implies 100^2+BC^2=135^2`

`\implies BC^2=135^2-100^2`

`\implies BC^2=8225`

`\implies BC=√(8225)`

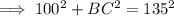
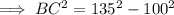
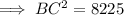
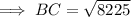
⇒ BC = 90.7 ft (nearest tenth)