Answer:
[-6,-3]
Explanation:
So we have the compound inequality:
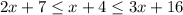
Let's solve for each of the inequalities:
1)
We have:

Subtract x from both sides:

Subtract 7 from both sides:
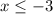
So that's one of our answers.
2)
We have:
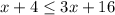
Subtract 3x from both sides:
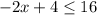
Subtract 4 from both sides:
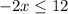
Divide both sides by -2. Since we're dividing by a negative, flip the sign:
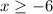
Therefore, our entire answer is:
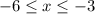
This means all values in between -3 and -6 including -3 and -6.
In interval notation, this is:
![[-6,-3]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ffi6ahhki6piy97bzkmb3bdv69iws63tg0.png)
So, A is -6.
And B is -3.
And we're done :)