Question

In humans there is a dominant allele (A) for the absence of moles; while the recessive allele (a) results in the presence of moles. A couple who are both heterozygous for this locus (Aa) plan to have seven children.

a. Expand the binomial (p + q)7.
b. What is the probability that:
(i) The first child that is born will not have moles.
(ii) All of the children will have moles.
(iii) The first two children will have no moles and the last five will have moles.
(iv) Of the 7 children, 4 will have no moles and 3 will have moles
c. Assume this couple now have two children, one with moles and one without moles. What is the probability that the child born without moles is a carrier of the a-allele (ie heterozygous)?

Answer 1

a.
`(p + q)^7` =
`p^7q^0+7p^6q+21p^5q^2+35p^4q^3+35p^3q^4+21p^2q^5+7pq^6+p^0q^7`

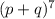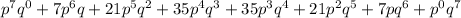
b. i. 0.75

ii. 0.000061

iii. 0.012

iv. 0.17

c. 0.67

Step-by-step explanation:

a. The expansion of the binomial (p + q)7 would be such that:

`(p + q)^7` =
`p^7q^0+7p^6q+21p^5q^2+35p^4q^3+35p^3q^4+21p^2q^5+7pq^6+p^0q^7`

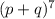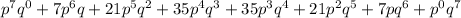
b. Both couples are heterozygous:

Aa x Aa

AA Aa Aa aa

Since A is dominant over a,

probability of having mole (aa) = 1/4

probability of not having moles = 3/4

Therefore, the probability of the first child not having moles = 3/4 or 0.75

ii. Let the probability of not having mole = p and the probability of having mole = q. From the binomial expansion:

`(p + q)^7` =
`p^7q^0+7p^6q+21p^5q^2+35p^4q^3+35p^3q^4+21p^2q^5+7pq^6+p^0q^7`

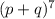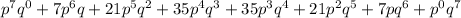
Probability that all of the children will have moles =
`p^0q^7`

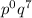
since p = 3/4 and q = 1/4

`p^0q^7` =
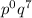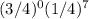`(3/4)^0(1/4)^7` = 0.000061

iii. Probability that the first two children will have no moles and the last five will have moles =
`21p^2q5`

=
`21(3/4)^2(1/4)^5`

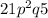
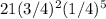
= 0.012

iv. Probability that 4 will have no moles and 3 will have moles out of the 7 children =
`35p^4q^3`

=
`35(3/4)^4(1/4)^3`

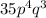
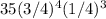
= 0.17

c. Probability that the child born without moles is a carrier of the a-allele = probability of heterozygous.

From the cross in (b), the genotypes of those born without moles are AA and 2Aa. Therefore, the probability of not having moles and be Aa is:

= 2/3 or 0.67