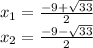Question

Solve x(x+9)+12=0 by using the Quadratic Formula.

Answer 1

Answer: approximately -1.63 and -7.37

Explanation:

First of all, let's expand the parenthesis by multiplying x into both of its terms.

`x(x+9)+12 = 0\\x^2+9x+12=0`

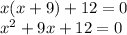
We get the equation:

`x^2+9x+12=0`

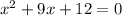
The quadratic formula looks like this

`$x=(-b\pm√(b^2-4ac))/(2a)$`

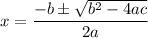
where the equation is of the form

`ax^(2)+bx+c=0`

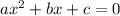
Comparing this to our equation above,

`x^2+9x+12=0`

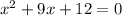
we can see that

`a = 1\\b= 9\\c= 12`

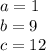
Let's put these values into the quadratic formula.

`x=(-b\pm√(b^2-4ac))/(2a)\\x=(-9\pm√(9^2-4*1*12))/(2*1)\\x=(-9\pm√(9^2-48))/(2)\\x=(-9\pm√(81-48))/(2)\\x=(-9\pm√(33))/(2)\\x=(-9\pm\ 5.744...)/(2)\\x=(-9\pm\ 5.744...)/(2)\\x_(1)=(-9+5.744...)/(2)=(-3.255...)/(2)=-1.62771867\\x_(2)=(-9-5.744...)/(2)=(-14.744...)/(2)=-7.3722813\\`

Answer: approximately -1.63 and -7.37

You can also choose not to approximate the square root of 33, and you'd receive the answers:

`x_(1)=(-9+√(33))/(2)\\x_(2)=(-9-√(33))/(2)`