Question

If someone could actually help me you will be so nice of you please I don’t understand this

Answer 1

So, the function is increasing over:
`(4,\infty)`

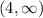
And it's decreasing over:
`(-\infty,4)`

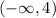
Explanation:

So first, let's graph the function. Please refer to the attached graph.

The function is increasing when the function is going upwards, and the function is decreasing when the function is going downwards.

From the graph, we can see that the function is going upwards after x=4. Therefore, the function is increasing for all values to the right of 4. In interval notation, this is:

`(4,\infty)`

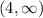
Also, we can see that the function is going downwards all the way from the left until x=4. Thus, the function is decreasing from for all values to the left of 4. In interval notation, this is:

`(-\infty,4)`

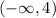
So, the function is increasing over:
`(4,\infty)`

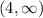
And it's decreasing over:
`(-\infty,4)`

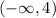
And those are our answers :)

Important Notes:

Note that we do not use brackets with the 4. This is because the function is only increasing to the right of 4 and decreasing to the left of 4. At exactly 4, the function is still; it is neither increasing nor decreasing. Thus, x equals exactly 4 will be in neither of our intervals.