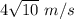Question

g a small smetal sphere, carrying a net charge is held stationarry. what is the speed are 0.4 m apart

Answer 1

The speed of q₂ is
`4√(10)\ m/s`

Step-by-step explanation:

Given that,

Distance = 0.4 m apart

Suppose, A small metal sphere, carrying a net charge q₁ = −2μC, is held in a stationary position by insulating supports. A second small metal sphere, with a net charge of q₂ = −8μC and mass 1.50g, is projected toward q₁. When the two spheres are 0.800m apart, q₂ is moving toward q₁ with speed 20m/s.

We need to calculate the speed of q₂

Using conservation of energy

`E_(i)=E_(f)`

`(1)/(2)mv_(i)^2+(kq_(1)q_(2))/(r_(i))=(kq_(1)q_(2))/(r_(f))+(1)/(2)mv_(f)^2`

`(1)/(2)m(v_(i)^2-v_(f)^2)=kq_(1)q_(2)((1)/(r_(f))-(1)/(r_(i)))`

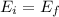
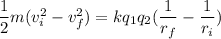
Put the value into the formula

`(1)/(2)*1.5*10^(-3)(20^2-v_(f)^2)=9*10^(9)*-2*10^(-6)*-8*10^(-6)((1)/((0.4))-(1)/((0.8)))`

`0.00075(400-v_(f)^2)=0.18`

`400-v_(f)^2=(0.18)/(0.00075)`

`-v_(f)^2=240-400`

`v_(f)^2=160`

`v_(f)=4√(10)\ m/s`

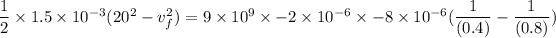
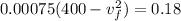
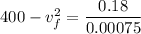
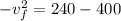
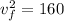
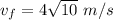
Hence, The speed of q₂ is
`4√(10)\ m/s`