Question

g What are the magnitude and direction of the electric field at a distance 43.5 mmmm from the center of the shells

Answer 1

Complete Question

Two spherical shells have a common center. A -1.6 x 10-6 C charge is spread uniformly over the inner shell, which has a radius of 0.030 m. A +5.1 x 10-6 C charge is spread uniformly over the outer shell, which has a radius of 0.15 m.What are the magnitude and direction of the electric field at a distance 43.5 mm from the center of the shells.

Answer:

The magnitude is
`E = 7.6021*10^(6) \N/C`

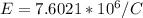
The direction is radially inward toward the center

Step-by-step explanation:

From the question we are told that

The charge on the inner shell is
`q_i = -1.6*10^(-6) \ C`

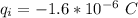
The radius of the inner shell is
`c_1 = 0.030 \ m`

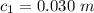
The charge on the outer shell is
`q_o = 5.1*10^(-6)\ C`

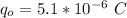
The radius of the outer shell is
`c_2 = 0.15\ m`

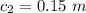
The distance considered is
`r = 43.5 \ mm = 0.0435 \ m`

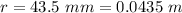
Generally the electric field at the position considered is mathematically represented as

`E = (Q_c )/(4\pi r^2 \epsilon_o )`

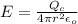
Here
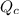`Q_c` is the charge which is enclosed by the distance considered which in this case is the charge on the inner shell

So
`Q_c =q_i = -1.6*10^(-6) \ C`

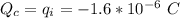
Hence

`E = (-1.6 *10^(-6) )/(4* 3.142 *0.0435^2* 8.85*10^(-12) )`

=>
`E = -7.6021*10^(6) \N/C`

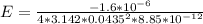
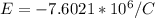
The negative sign is show that the direction of the field is radially inward toward the center