Question

The length of one leg of the right triangle is 2 ft less than the length of the hypotenuse. The length of the other leg is 1 ft less than the length of the hypotenuse. Find the length of the sides.

Answer 1

The length of the sides are 3 feet and 4 feet, respectively.

Explanation:

Given the fact that triangle is a right triangle, it can be represented by Pythagorean Theorem:

`r^(2) = x^(2)+y^(2)`

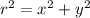
Where:

`r` - Hypotenuse, measured in feet.

`x`,
`y` - Legs, measured in feet.

In addition, each leg can be determined as functions of hypotenuse:

`x = r-2\,ft`

`y = r-1\,ft`

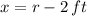
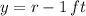
Hence, the Pythagorean identity can be expanded and remaining variable may be solved:

`r^(2) = (r-2\,ft)^(2)+(r-1\,ft)^(2)`

`r^(2) = r^(2)-4\cdot r +4 + r^(2)-2\cdot r +1`

`r^(2)-6\cdot r +5 =0`

`(r-5)\cdot (r-1) = 0`

`r = 5\,ft\,\vee\,r = 1\,ft`

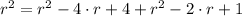
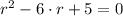
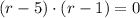
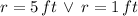
According to the definition of hypotenuse, it must be longer than any of legs. Hence, there is just one solution that is reasonable:

`r = 5\,ft`

And length of the sides are, respectively:

`x = 5\,ft-2\,ft`

`x =3\,ft`

`y = 5\,ft-1\,ft`

`y = 4\,ft`

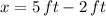
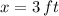
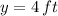
The length of the sides are 3 feet and 4 feet, respectively.