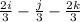Question

Find the magnitude of u × v and the unit vector parrallel to u × v in the direction of u × v. u = 2i + 2j - k, v = -i + k

Answer 1

magnitude = 3

unit vector =
`(2i)/(3) - (j)/(3) - (2k)/(3)`

Step-by-step explanation:

Given vectors:

u = 2i + 2j - k

v = -i + k = -i + 0j + k

(a) u x v is the cross product of u and v, and is given by;

`u X v = \left[\begin{array}{ccc}i&j&k\\2&2&-1\\-1&0&1\end{array}\right]`

u x v = i(2+0) - j(2 - 1) + k(0 - 2)

u x v = 2i - j - 2k

Now the magnitude of u x v is calculated as follows:

| u x v | =
`√(2^2 + (-1)^2 + (-2)^2)`

| u x v | =
`√(4 + 1 + 4)`

| u x v | =
`√(9)`

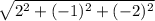
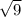
| u x v | = 3

Therefore, the magnitude of u x v is 3

(b) The unit vector û parallel to u x v in the direction of u x v is given by the ratio of u x v and the magnitude of u x v. i.e

û =
`(u X v)/(|u X v|)`

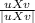
u x v = 2i - j - 2k [calculated in (a) above]

|u x v| = 3 [calculated in (a) above]

∴ û =
`(2i - j - 2k)/(3)`

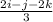
∴ û =
`(2i)/(3) - (j)/(3) - (2k)/(3)`