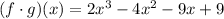Answer:
1)
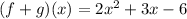
2)
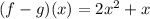
3)
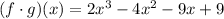
Explanation:
So we have the two functions:
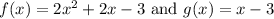
And we want to find (f+g)(x), (f-g)(x), and (f*g)(x).
1)
(f+g)(x) is the same to f(x)+g(x). Substitute:
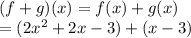
Combine like terms:
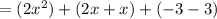
Add:
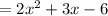
So:
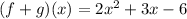
2)
(f-g)(x) is the same to f(x)-g(x). So:
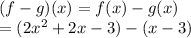
Distribute:
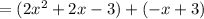
Combine like terms:
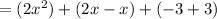
Simplify:
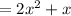
So:
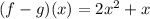
3)
(f*g)(x) is the same to f(x)*g(x). Thus:
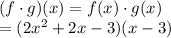
Distribute:
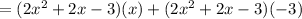
Distribute:
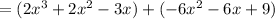
Combine like terms:
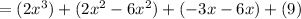
Simplify:
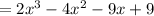
So: