Question

Use a definite integral to find the area of the region between the given curve and the​ x-axis on the interval [0, b].y= 2x^2.

Answer 1

Given :

Given a curve ,
`y=2x^2` .

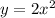To Find :

The area of the region between the given curve and the​ x-axis on the interval [0, b] .

Solution :

Now , area under the curve is given by :

`A=\int\limits^b_0 {2x^2} \, dx \\\\A= |_0^b((2)/(3)x^((2+1)))\\\\A=(2b^3)/(3)`

( Integration of
`x^2` is
`(x^3)/(3)` )

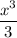Therefore , the region between the given curve and the​ x-axis on the interval [0, b] is
`(2b^3)/(3)` .

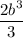Hence , this is the required solution .