Question

Find the length of the missing side of the right triangle.​

Answer 1

Here you are trying to find the hypotenuse. So you would take
5^2 (five squared) plus 12^2 (twelve squared) and add them using the equation a^2+b^2= c^2. Now you square 5 and 12 to get 25 and 144. You add them together and get 169. Take the square root of 169 and c. The square root on c will cancel out the squared (to the power of two) part leaving you with just c. And the square root of 169 is 13. So c (the missing length) is 13. C=13.

Answer 2

`\boxed{ \bold{ \huge{ \boxed{ \sf{13 \: \: units \: }}}}}`

Explanation:

Perpendicular ( p ) = 5

Base ( b ) = 12

Hypotenuse ( h ) = ?

Finding the length of missing side

Using Pythagoras theorem

`\boxed{ \sf{ {h}^(2) = { p}^(2) + {b}^(2) }}`

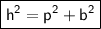
plug the values

⇒
`\sf{ {h}^(2) = {5}^(2) + {12}^(2) }`

Evaluate the power

⇒
`\sf{ {h}^(2) = 25 + 144}`

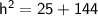
Add the numbers : 25 and 144

⇒
`\sf{ {h}^(2) = 169}`

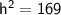
Squaring on both sides

⇒
`\sf{ \sqrt{ {h}^(2) } = √(169)}`

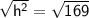
Calculate

⇒
`\sf{ {h} = 13 \: units}`

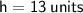
Hope I helped!

Best regards! :D