Answer:
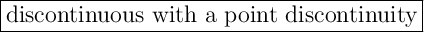
![\rule[225]{225}{2}](https://img.qammunity.org/2021/formulas/chemistry/middle-school/ri1osubq0ul0fyszs3s2hvchlv85n22xxb.png)
Explanation:
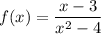
When x = 2.
We can see that the denominator is equal to 0 when the input value is 2.
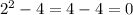
Obtaining a zero in the denominator indicates a point of discontinuity.
In the graph below, we can see that the function is discontinuous at x = 2.
![\rule[225]{225}{2}](https://img.qammunity.org/2021/formulas/chemistry/middle-school/ri1osubq0ul0fyszs3s2hvchlv85n22xxb.png)