Answer:
D
Explanation:
The area of a rectangle is given by the formula:
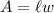
So, we are given that the area is:

And the width is:
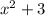
And we want to find the length. To do so, first substitute the expressions into the equation:
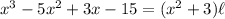
Thus, to find the length, divide by (x²+3):
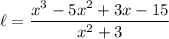
We can factor the numerator:

From the first two terms, factor out a x².
From the third and fourth terms, factor out a 3:
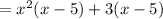
Combine:
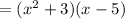
Putting this back:
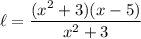
Cancel:
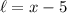
Hence, our answer is D.