Question

What is the toy's total energy at any point of its motion? Express your answer with the appropriate units.]

Answer 1

The complete question is as follows:

A 0.150-kg toy is undergoing SHM on the end of a horizontal spring with force constant k = 300 N/m. When the toy is 0.0120 m from its equilibrium position, it is observed to have a speed of 0.400 m/s.

Answer:

The correct answer is 0.034 J.

Step-by-step explanation:

Given :

mass of the toy is m = 0.15 kg.

The force constant of restoring force k = 300 Nm⁻¹

When the position of the toy from the equilibrium is x = 0.012m, then the

speed of the toy vx = 0.4m s

The total mechanical energy in SHM is given by

E= 1/2 (mv²+ kx²) = 1/2 kA²

(here, m = mass of the object, vx = velocity, k = force constant

of restoring force, and A = amplitude of SHM.)

Hence by substituting the numerical values in equation 1, we get

`E= (1)/(2) (0.15* 0.4) + (1)/(2) (300* 0.012)`

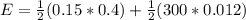
= 0.034 J

Thus, the correct answer is 0.034 J.