Question

Find the angle between the vectors a = (4, 2, -4) and b = (4, -3, 2).

SOLUTION Since
lal = 42 + 22 + (-4)2 =
and
[b] = V 42 + (-3)2 + 22 = V 29
and since
a. b = (4)( 14 ) + (2)(-3) + (-4)(2 )
we have from this corollary
COS = a.b |а|
|Ь| | 89 So the angle between a and b is as follows. (Round your final answer to two decimal places.) 0 = cos-10 29 89 x rad

Answer 1

86.45°

Explanation:

Given two vectors a = (4, 2, -4) and b = (4, -3, 2), the formula to be used to calculate the angles between both vectors is as expressed below;

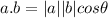`a.b = |a||b| cos \theta` where
`\theta` is the angle between both vectors

a.b = (4, 2, -4). (4, -3, 2)

a.b = 4(4)+2(-3)+2(-4)

a.b = 16-6-8

a.b = 16-14

a.b = 2

Given |r| = √x²+y²+z²

|a| = √4²+2²+(-4)²

|a| = √16+4+16

|a| = √36

|a| = 6

Similarly;

|b| = √4²+(-3)²+2²

|b| = √16+9+4

|b| = √29

Substituting the parameters gotten into the formula to get the angle between the two vectors a and b we will have;

`a.b = |a||b| cos \theta\\2 = 6*√(29) \ cos \theta\\ cos\theta = (2)/(6√(29) ) \\cos\theta = (1)/(3√(29) )\\ cos\theta = 0.0619\\\theta = cos ^(-1)0.0619\\ \theta = 86.45^0 (to \ 2dp)`

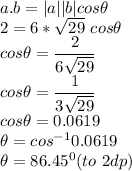
Hence the angle between vectors a and b is 86.45°