Question

The following data represent the pH of rain for a random sample of 12 rain dates. A normal probability plot suggests the data could come from a population that is normally distributed.

5.20, 5.02, 4.87, 5.72, 4.57, 4.76, 4.99, 4.74, 4.56, 4.80, 5.19, 4.68
1) Determine a point estimate for the population mean.
2) Construct and Interpret a 95% confidence interval for the mean pH of rainwater.
a) if repeated samoles are taken, 95% of them will have a sample pH of rain water between [ ] & [ ].
b) there is a 95% chance that the true mean pH of rain water is between [ ] & [ ].
c) there is 95% confidence that the population mean pH of rain water is between [ ] & [ ].
3) Construct and interpret a 99% confidence interval for the mean pH of rainwater.
a) there is 99% confidence that the population mean pH of rain water is between [ ] & [ ].
b) there is a 99% chance that the true mean pH of rain water is between [ ] & [ ].
c) if repeated samoles are taken, 99% of them will have a sample pH of rain water between [ ] & [ ].
4) What happens to the interval as the level of confidence is changed? Explain why is a logical result.
As the level of confidence increases l, the width of the interval_____this makes sense since the_____,______.

Answer 1

(1) The point estimate for the population mean is 4.925.

(2) Therefore, a 95% confidence interval for the population mean pH of rainwater is [4.715, 5.135] .

(3) Therefore, a 99% confidence interval for the population mean pH of rainwater is [4.629, 5.221] .

(4) As the level of confidence increases, the width of the interval increases.

Explanation:

We are given that the following data represent the pH of rain for a random sample of 12 rain dates.

X = 5.20, 5.02, 4.87, 5.72, 4.57, 4.76, 4.99, 4.74, 4.56, 4.80, 5.19, 4.68.

(1) The point estimate for the population mean is given by;

Point estimate,
`\bar X` =
`(\sum X)/(n)`

=
`(5.20+5.02+ 4.87+5.72+ 4.57+ 4.76+4.99+ 4.74+ 4.56+ 4.80+5.19+ 4.68)/(12)`

=
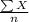
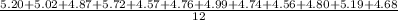
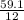`(59.1)/(12)` = 4.925

(2) Let
`\mu` = mean pH of rainwater

Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;

P.Q. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean = 4.925

s = sample standard deviation = 0.33

n = sample of rain dates = 12

`\mu` = population mean pH of rainwater

Here for constructing a 95% confidence interval we have used a One-sample t-test statistics as we don't know about population standard deviation.

So, 95% confidence interval for the population mean,
`\mu` is ;

P(-2.201 <
`t_1_1` < 2.201) = 0.95 {As the critical value of t at 11 degrees of

freedom are -2.201 & 2.201 with P = 2.5%}

P(-2.201 <
`(\bar X-\mu)/((s)/(√(n) ) )` < 2.201) = 0.95

P(
`-2.201 * {(s)/(√(n) ) }` <
`{\bar X-\mu}` <
`2.201 * {(s)/(√(n) ) }` ) = 0.95

P(
`\bar X-2.201 * {(s)/(√(n) ) }` <
`\mu` <
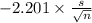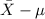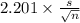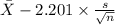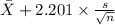`\bar X+2.201 * {(s)/(√(n) ) }` ) = 0.95

95% confidence interval for
`\mu` = [
`\bar X-2.201 * {(s)/(√(n) ) }` ,
`\bar X+2.201 * {(s)/(√(n) ) }` ]

= [
`4.925-2.201 * {(0.33)/(√(12) ) }` ,
`4.925+2.201 * {(0.33)/(√(12) ) }` ]

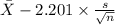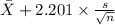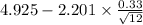= [4.715, 5.135]

Therefore, a 95% confidence interval for the population mean pH of rainwater is [4.715, 5.135] .

The interpretation of the above confidence interval is that we are 95% confident that the population mean pH of rainwater is between 4.715 & 5.135.

(3) Now, 99% confidence interval for the population mean,
`\mu` is ;

P(-3.106 <
`t_1_1` < 3.106) = 0.99 {As the critical value of t at 11 degrees of

freedom are -3.106 & 3.106 with P = 0.5%}

P(-3.106 <
`(\bar X-\mu)/((s)/(√(n) ) )` < 3.106) = 0.99

P(
`-3.106 * {(s)/(√(n) ) }` <
`{\bar X-\mu}` <
`3.106 * {(s)/(√(n) ) }` ) = 0.99

P(
`\bar X-3.106 * {(s)/(√(n) ) }` <
`\mu` <
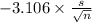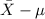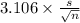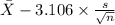`\bar X+3.106 * {(s)/(√(n) ) }` ) = 0.99

99% confidence interval for
`\mu` = [
`\bar X-3.106 * {(s)/(√(n) ) }` ,
`\bar X+3.106 * {(s)/(√(n) ) }` ]

= [
`4.925-3.106 * {(0.33)/(√(12) ) }` ,
`4.925+3.106 * {(0.33)/(√(12) ) }` ]

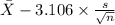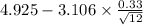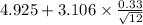= [4.629, 5.221]

Therefore, a 99% confidence interval for the population mean pH of rainwater is [4.629, 5.221] .

The interpretation of the above confidence interval is that we are 99% confident that the population mean pH of rainwater is between 4.629 & 5.221.

(4) As the level of confidence increases, the width of the interval increases as we can see above that the 99% confidence interval is wider as compared to the 95% confidence interval.