Question

Two asteroids identical to those above collide at right angles and stick together; i.e, their initial velocities were perpendicular to each other (take A initially moving to the right and B initially moving up). Use momentum conservation (make a complete Momentum Chart) to find the velocity (magnitude and direction with-respect-to the velocity asteroid A had before the collision) of the asteroids after the collision.

Answer 1

velocity = 62.89 m/s in 58 degree measured from the x-axis

Step-by-step explanation:

Relevant information:

Before the collision, asteroid A of mass 1,000 kg moved at 100 m/s, and asteroid B of mass 2,000 kg moved at 80 m/s.

Two asteroids moving with velocities collide at right angles and stick together. Asteroid A initially moving to right direction and asteroid B initially move in the upward direction.

Before collision Momentum of A = 1000 x 100 =
`$ 10^5$` kg - m/s in the right direction.

Before collision Momentum of B = 2000 x 80 = 1.6 x
`$ 10^5$` kg - m/s in upward direction.

Mass of System of after collision = 1000 + 2000 = 3000 kg

Now applying the Momentum Conservation, we get

Initial momentum in right direction = final momentum in right direction =
`$ 10^5$`

And, Initial momentum in upward direction = Final momentum in upward direction = 1.6 x
`$ 10^5$`

So,
`$ V_x = (10^5)/(3000) $` =
`$ (100)/(3) $` m/s

and
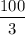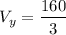`$ V_y=(160)/(3)$` m/s

Therefore, velocity is =
`$ √(V_x^2 + V_y^2) $`

=
`$ \sqrt{((100)/(3))^2 + ((160)/(3))^2} $`

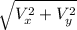
= 62.89 m/s

And direction is

tan θ =
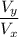`$ (V_y)/(V_x)$` = 1.6

therefore,
`$ \theta = \tan^(-1)1.6 $`

=
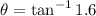
`$ 58 ^(\circ)$` from x-axis