Question

A drone is launched with a velocity of 63 m/s, 29 . Three minutes after the drone is launched it suddenly changed its course to 22 m/s, 233 to avoid high trees on its way. Then, it finally goes back at a rate of 98 m/s, 321. Calculate for the total resultant vector of the drone.

Answer 1

v = 127.66 m / s θ’= 337.59

Step-by-step explanation:

For this exercise we must use the speed composition of the drone.

The first speed is 63 m / s in direction 29, three minutes later the speed reaches 22 m / s and direction 233, finally it returns to the launch point with 98 m / s in direction 321, in the attachment you can see a diagram of these speeds.

To find the resulting average velocity, the easiest thing is to decompose each velocity into the x and y coordinate system, then add each velocity

let's break down the speeds

cos 29 = v₁ₓ / v₁

sin 29 =
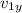`v_(1y)` / v₁

v₁ₓ = v₁ cos 29

v_{1y} = v₁ sin 29

v₁ₓ = 63 cos 29 = 55.10 m / s

v_{1y} = 63 sin 29 = 30.54 m / s

speed 2

cos 22 = v₂ₓ / v₂

sin 22 = v_{2y} / v₂

v₂ₓ = v₂ cos 233

v_{2y} = v₂ sin 233

v₂ₓ = 22 cos 233 = -13.24 m / s

v_{2y} = 22 sin 233 = -17.57 m / s

speed 3

cos 321 = v₃ₓ / v₃

sin 321 = v_{3y} / v₃

v₃ₓ = v₃ cos 321

v_{1y} = vₐ sin 321

v₃ₓ = 98 cos 321 = 76.16 m / s

v_{3y} = 98 sin 321 = -61.67 m / s

We already have all the component of the speeds, the resulting speed is

vₓ = v₁ₓ + v₂ₓ + v₃ₓ

vₓ = 55.10 -13.24 +76.16

vₓ = 118.02 m / s

v_{y} = v_{1y} + v_{2y} + v_{3y}

v_{y} = 30.54 -17.54 - 61.67

v_{y} = -48.67 m / s

there are two ways to give the result

v = (118.02 i -48.67 j) m / s

or in the form of magnitud and angle.

We use the Pythagorean theorem for the module

v = √ (vₓ² + v_{y}²)

v = RA (118.02² + 48.67²)

v = 127.66 m / s

let's use trigonometry for the angle

tan θ = v_{y} / vₓ

θ = tan⁻¹ (v_{1} / vₓ)

θ = tan⁻¹ (-48.67 / 118.02)

θ = -22.41

if we want to measure the angles with respect to the positive side of the x axis

θ’= 360 - 22.41

θ’= 337.59