Question

Find the sum of first 20 terms of the arithmetic series in which 3rd term is 7 and 7th term is 2 more than three times its 3rd term.

Answer 1

740

Explanation:

Let the AP be a, a+d, a+2d, a+3d, ...

The term of AP is given by:

`t n =a+(n-1)d`

We are given that the third term is 7.

`t 3=7`

⇒
`a+(3-1)d=7`

⇒
`a+2d=7 ---(1)`

Also, the seventh term is 2 more than three times the third term.

`t7=3t3+2`

⇒
`a+ (7-1)d=3(a+(3-1)d)+2`

⇒
`a+6d=3(a+2d)+2`

⇒
`a+6d=3a+6d+2`

⇒
`-2a=2`

⇒
`a=-1`

We can put it in (1)

`a+2d=7`

⇒
`(-1)+2d=7`

⇒
`2d=8`

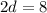
⇒d=4

Now, the Sum of n terms of an AP is given by the formula:

`sn=(n)/(2)(2a+(n-1)d)`

So, Sum of first 20 terms would be:

`s 20=(20)/(2)(2(-1) +(20-1) x 4)`

⇒
`s20=10(-2+19 x 4)`

⇒
`s 20=10 x(-2+76)`

⇒
`s 20= 10 x 74`

⇒
`s 20=740`

Thus, The Sum of first 20 terms of the AP is 740.